VAE做了什么
直观解释VAE
一、用VAE解决什么问题?
生成模型是当今机器学习研究领域的一大热点。变分自编码器(VAE)就是一种生成式模型。它通过非监督学习,得到一个模型。这个模型可以基于用户的输入生成未在数据集中出现过的内容。
在机器学习中,经常把样本抽象为高维向量。对于每个类别都存在着一个概率分布,这个分布中的每个点代表着某个高维向量属于该类别的概率。
那么,我们只要知道这个概率分布是什么样的,就可以生成高概率的高维向量,这样就可以生成新的样本了。
VAE就是一种基于标准函数逼近器(神经网络)而设计出来的模型,可以用来逼近和描述概率分布。
二、VAE如何生成内容?
VAE的结构是什么样的?是如何完成逼近某个概率分布的功能的?
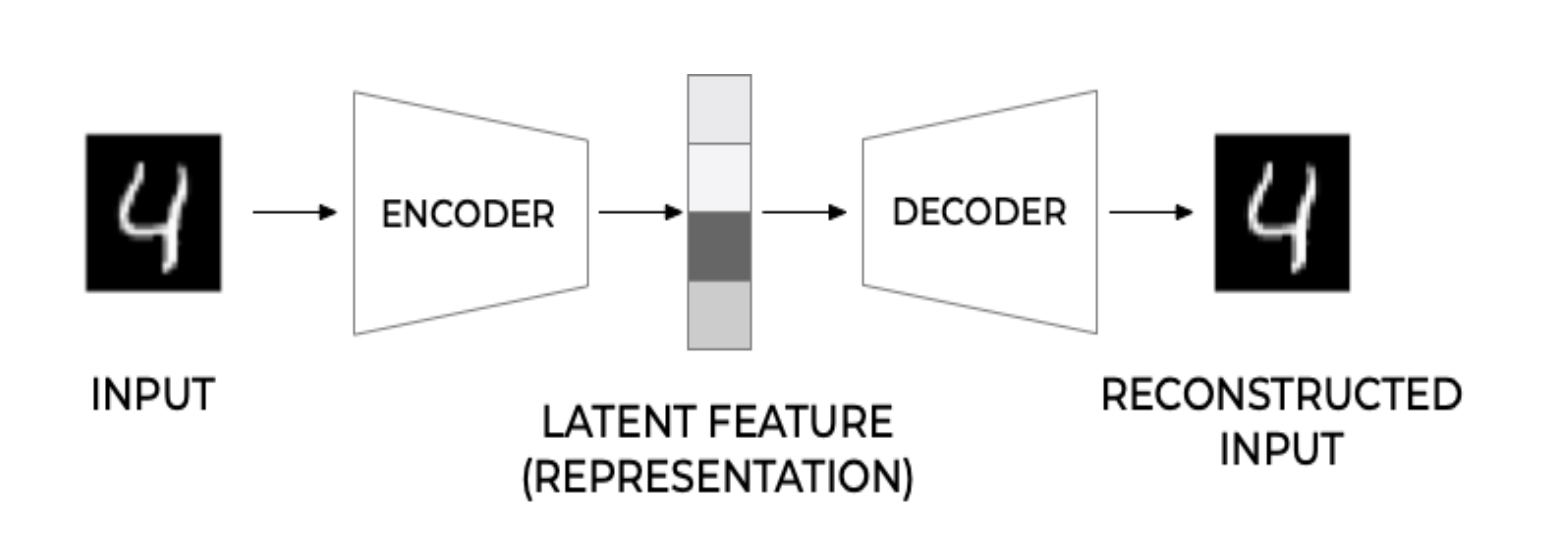
在了解VAE之前,先了解以下AE(autoencoder)。
VAE的结构与其相似,不同的是VAE编码器(decoder)学习到的这个函数可以根据输入得到一个隐变量的分布,即由$x$得到$\mu^\prime(x)$和$\Sigma^\prime(x)$。可参考下图中的左图。
对于生成任务来说,编码器的功能是为了找到能够在较为低维的空间中找到样本$x$的向量。在训练完成之后,编码器就没有什么用了。之后保留解码器来做生成任务即可。 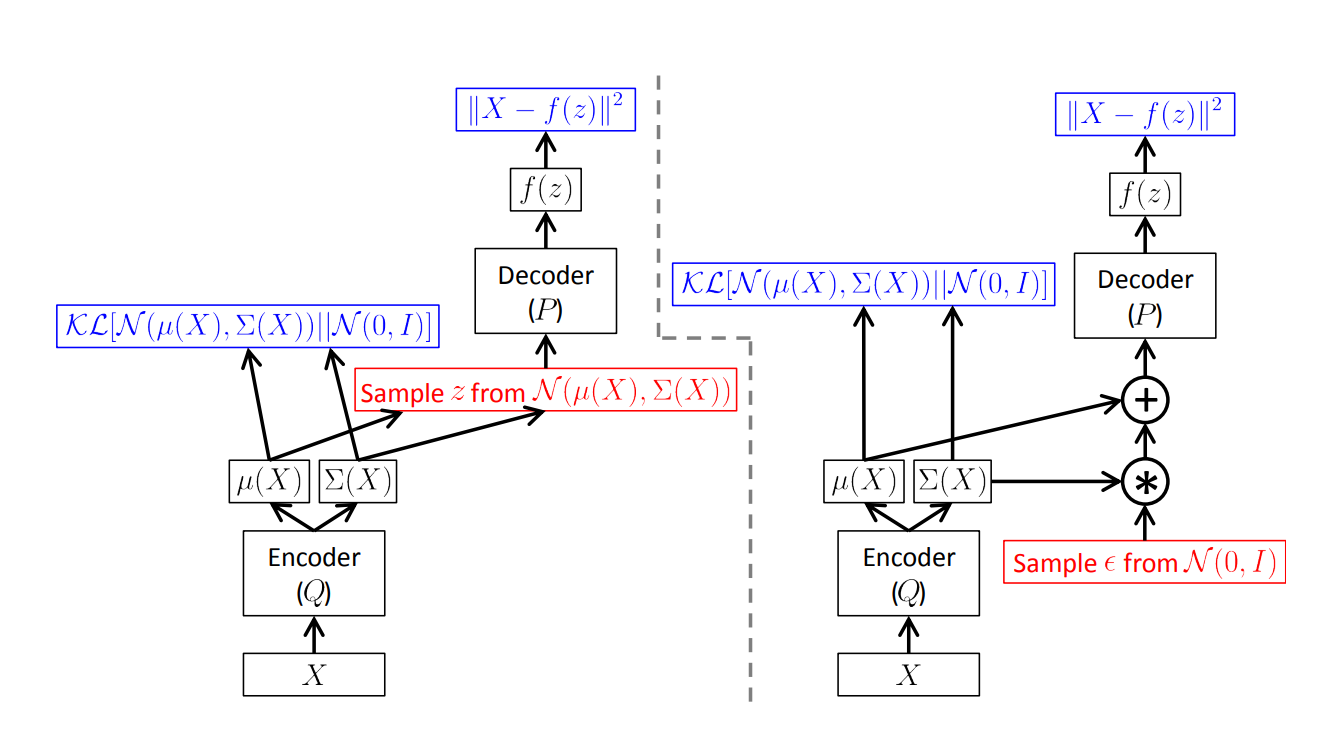
在VAE中,就是借助解码器和编码器(神经网络)来逼近前文中提到的某个概率分布$P(x)$。
在高等数学中,我们经常用泰勒展开来逼近某个函数来解决问题,因为多项式在该空间中表现力强可以用来近似某个函数。同样的,一组高斯分布也可以用来近似函数。
混合高斯分布 一元高斯分布: \(X \sim \mathcal{N}(\mu,\,\sigma^{2})\,\)
\[\mathcal{N}(\mu,\,\sigma^{2}) = \frac{1}{\sqrt{2\pi\sigma^2}}exp(\frac{-(x-\mu)^2}{2\sigma^2})\]多元高斯分布:
\[X \sim \mathcal{N}(\mu,\,\Sigma)\,\] \[\mathcal{N}(\mu,\,\Sigma) = \frac{1}{(2\pi)^{\frac{n}{2}}det(\Sigma)^{\frac{1}{2}}}exp(\frac{-(x-\mu)^{T}\Sigma^{-1}(x-\mu)}{2})\],其中$\Sigma$是协方差矩阵。 由n个不同参数的多元高斯函数及其权重线性组合而成一个混合高斯分布:
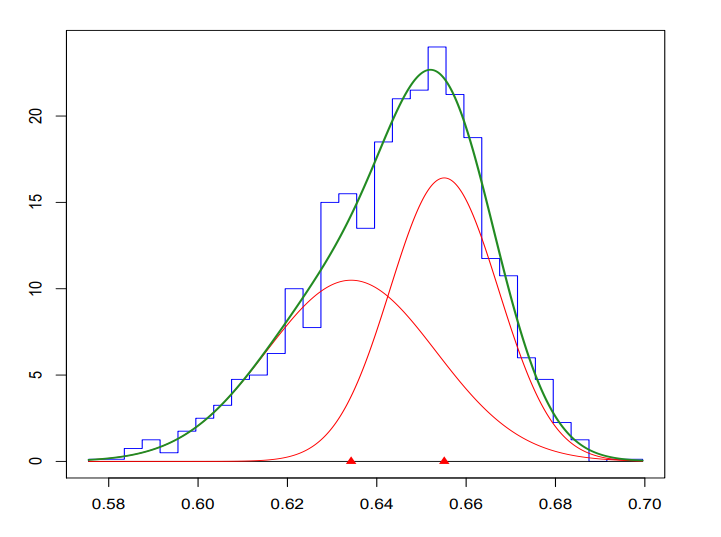
\(P(x) = \sum_{i=1}^{n} w_i \cdot \mathcal{N}(x|\mu_i, \Sigma_i)\) 例如下图中用两个高斯函数来拟合一个函数:
但是由离散的高斯函数进行的混合表现力和拟合能力不够强,因此就把这种混合从离散拓展到连续上:
\[P(x) = \int_{z}p(z)p(x|z)dz\]其中$p(x|z)$就是在给定$z$情况的下的高斯分布,$z$就是隐变量。
上式也是全概率分布的连续形式,无论$z$的分布如何都不会影响该式成立。此时,在数学上就把求$P(x)$的问题转化成求$p(x|z)$。
但是在训练解码器的过程中,必须要知道$p(z)$是什么样的,求得$p(z)$的工作就由编码器来实现。
在训练VAE模型的理想情况下,我们尽量避免手动去决定$z$的哪个维度是编码哪些信息的,也不希望显示描述$z$的维度之间的依赖关系。
所以VAE采用了以下这种方法:
用编码器根据$x$得到与之对应的分布$p(z)$,这是一个高斯分布,他的参数是$\mu^\prime(x)$和$\Sigma^\prime(x)$。
随后,从标准的正态分布中进行采样,
\[a \sim \mathcal{N}(0,\,I)\]其中,$I$是单位矩阵,$a$的每个维度都代表着一个属性(attribute)。
再将采样出来的变量映射到隐变量$z$上,这个方法是逆变换采样的一种延生。
逆变换采样
在进行仿真的时候,有时无法用计算机直接对比较复杂的分布进行采样。 假设其PDF为$f(x)$。由于这个是一个概率,所以它的CDF$F(x)$是在$\left[0,1\right]$之间。
因此可以在0到1之间进行均匀的采样:
\[a \sim U\left(0,1\right)\]之后,在根据$F(x)$的逆函数来求得所需要的样本:
\[a^* = F^{-1}(a)\]
在VAE中,通常用这样映射:
\[z = \mu^\prime(x) + \Sigma^\prime(x) \times a\]那么,以什么目标训练这个网络?
Maximizing Likelihood
在VAE中,训练目标就是找到最大的
\[L= \displaystyle\sum_x logP(x)\]接下来对上式进行变形:
\[logP(x) = \int_{z}q(z|x)logP(x)dz = \int_{z}q(z|x)log\left( \frac{P(z,x)}{P(z|x)} \right)dz \\= \int_{z}q(z|x)log\left( \frac{P(z,x)}{P(z|x)} \frac{q(z|x)}{q(z|x)} \right)dz = \int_{z}q(z|x)log\left( \frac{P(z,x)}{q(z|x)} \right)dz + \int_{z}q(z|x)log\left( \frac{q(z|x)}{P(z|x)} \right)dz\]可以发现,变形后式子的最后一项是KL散度:
\[\int_{z}q(z|x)log\left( \frac{q(z|x)}{P(z|x)} \right)dz = KL(q(z|x)||P(z|x))\]KL散度用于衡量两个概率分布的之间的差异程度,是非负的,因此原式必然
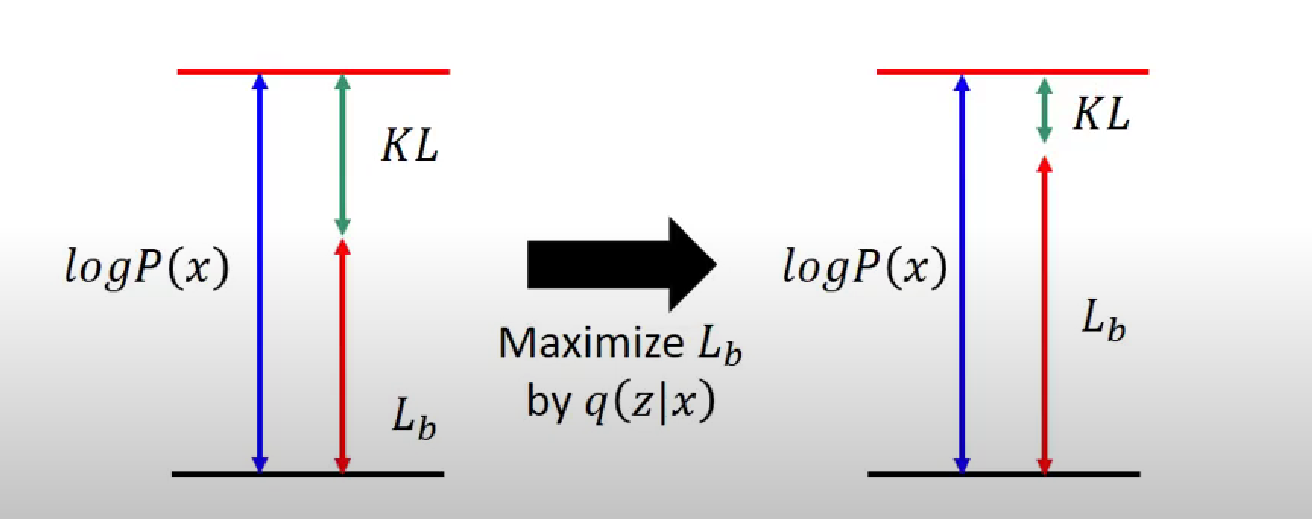
\[\geq \int_{z}q(z|x)log\left( \frac{P(z,x)}{q(z|x)} \right)dz = \int_{z}q(z|x)log\left( \frac{P(x|z)P(z)}{q(z|x)} \right)dz\]于是,上式就是$logP(x)$的下界(lower bound),记作$L_b$。所以,现在通过优化${q(z|x)}$来找到最大的$L_b$。
由于之前我们在变形的时候同时乘上并且除以${q(z|x)}$,因此通过调整${q(z|x)}$来最大化$L_b$时,不会影响$\log(P(x))$的大小,并且随着$L_b$的增大$KL$散度还会减小,这意味着${q(z|x)}$和${P(z|x)}$之间的差异也会来越小:
\[L_b = \int_{z}q(z|x)log\left( \frac{P(x|z)P(z)}{q(z|x)} \right)dz \\= \int_{z}q(z|x)log\left( \frac{P(z)}{q(z|x)} \right)dz + \int_{z}q(z|x)log{P(x|z)}dz\]再次拆开两式之后发现
\[\int_{z}q(z|x)log\left( \frac{P(z)}{q(z|x)} \right)dz = -KL(q(z|x)||P(z))\]现在要做两件事:
1.最小化 ${KL(q(z|x) | |P(z))}$
在神经网络中,调节$q(z|x)$对应着调节编码器的神经网络,当$q(z|x)$越接近正态分布时,他们之间就越接近。详情请参考以下链接的附录2. Auto-Encoding Variational Bayes
2.最大化$\int_{z}q(z|x)log{P(x|z)}dz$
\[\int_{z}q(z|x)log{P(x|z)}dz = E_{q(z|x)}(logP(x|z))\]根据期望的公式,可以理解为在分布$q(z|x)$上对$P(x|z)$进行加权平均。此时我们要通过训练神经网络让这个值最大。
三、VAE的优点和缺点
优点
1.可以学习出数据的潜在分布
2.是一种无监督学习
缺点
1.生成的对象只是训练集的线性组合,生成的质量不好。
2.训练时,的目标只在乎和输入是否一致,并没有评估生成对象质量的好坏。